В геометрии понятие неразвернутых углов играет важную роль при изучении различных фигур и их свойств. Рассмотрим подробно, чему равна сумма таких углов в различных геометрических конфигурациях.
Содержание
В геометрии понятие неразвернутых углов играет важную роль при изучении различных фигур и их свойств. Рассмотрим подробно, чему равна сумма таких углов в различных геометрических конфигурациях.
Определение неразвернутого угла
Неразвернутым углом называется угол, величина которого меньше 180 градусов. Это означает:
- Угол больше 0°, но меньше 180°
- Не является прямым (90°) или развернутым (180°) углом
- Может быть острым (меньше 90°) или тупым (больше 90°)
Сумма неразвернутых углов в треугольнике
| Тип треугольника | Сумма углов | Особенности |
| Остроугольный | 180° | Все три угла неразвернутые и острые |
| Прямоугольный | 180° | Два неразвернутых угла (острые) |
| Тупоугольный | 180° | Два неразвернутых угла (один тупой, два острых) |
Сумма неразвернутых углов в многоугольниках
Выпуклые многоугольники
Для выпуклого n-угольника сумма внутренних углов вычисляется по формуле:
- S = (n - 2) × 180°
- Все углы являются неразвернутыми
Невыпуклые многоугольники
- Сумма углов также равна (n - 2) × 180°
- Могут содержать развернутые углы (180°)
- Сумма только неразвернутых углов: S = (n - 2) × 180° - k × 180°, где k - количество развернутых углов
Особые случаи
Четырехугольники
- Сумма внутренних углов: 360°
- Если все углы неразвернутые: 4 угла < 180° каждый, но сумма 360°
- Максимальный неразвернутый угол в четырехугольнике: менее 360°
Пятиугольники
- Сумма внутренних углов: 540°
- Максимальное количество неразвернутых углов: 5
- Максимальная сумма неразвернутых углов: менее 5 × 180° = 900°
Практическое применение
| Область | Значение суммы неразвернутых углов |
| Архитектура | Расчет углов при проектировании конструкций |
| Компьютерная графика | Моделирование трехмерных объектов |
| Навигация | Определение курсов и маршрутов |
Геометрические доказательства
Для треугольника
Через любую вершину треугольника проведем прямую, параллельную противоположной стороне. Образовавшиеся углы составляют в сумме 180°, что доказывает теорему о сумме углов треугольника.
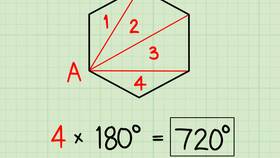
Для n-угольника
Разобьем многоугольник на (n - 2) треугольника. Поскольку сумма углов каждого треугольника 180°, общая сумма будет (n - 2) × 180°.
Важные выводы
- Сумма неразвернутых углов в треугольнике всегда равна 180°
- В выпуклом многоугольнике все углы неразвернутые, их сумма (n - 2) × 180°
- В невыпуклых фигурах сумма неразвернутых углов зависит от количества развернутых углов
- Максимальный неразвернутый угол всегда меньше 180°
Понимание свойств суммы неразвернутых углов является фундаментальным для решения геометрических задач и находит применение во многих практических областях.
