Сумма внутренних углов треугольника - это фундаментальное свойство евклидовой геометрии, которое справедливо для всех треугольников независимо от их вида и размеров. Данное свойство имеет важное значение в геометрии и находит практическое применение в различных расчетах.
Содержание
Сумма внутренних углов треугольника - это фундаментальное свойство евклидовой геометрии, которое справедливо для всех треугольников независимо от их вида и размеров. Данное свойство имеет важное значение в геометрии и находит практическое применение в различных расчетах.
Основная теорема
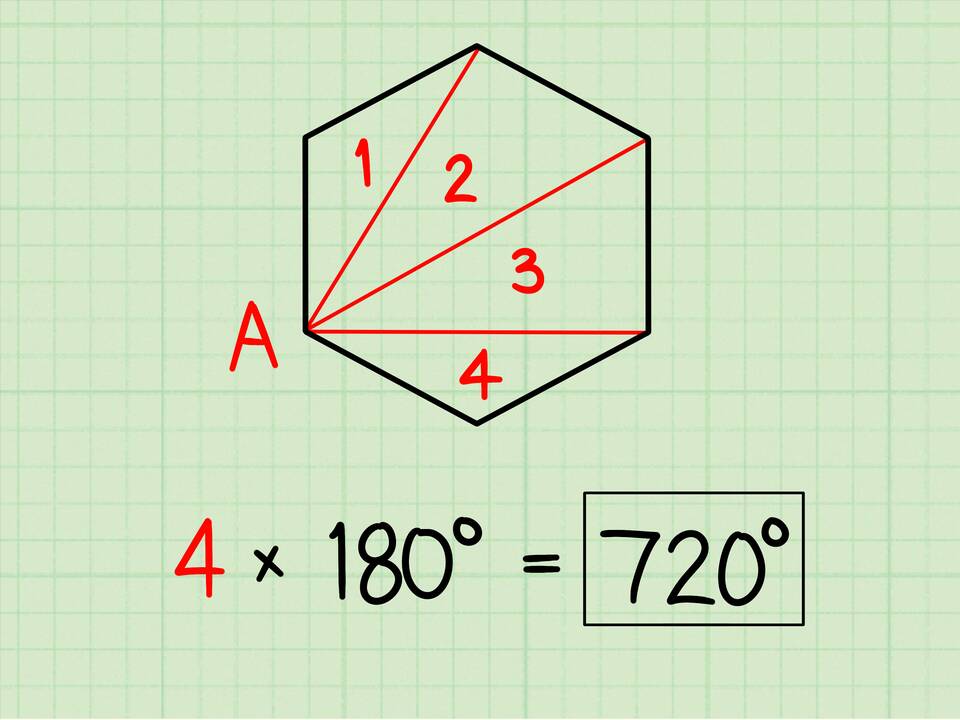
Сумма внутренних углов любого треугольника равна 180 градусам (или π радианам). Это можно выразить формулой:
∠A + ∠B + ∠C = 180°
Доказательство теоремы
Классическое доказательство
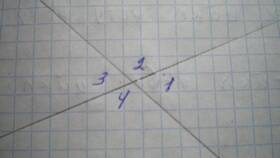
- Проведем через вершину B прямую, параллельную стороне AC
- Углы 1 и 4 равны как накрест лежащие
- Углы 3 и 5 равны как накрест лежащие
- Углы 4, 2 и 5 образуют развернутый угол (180°)
- Следовательно, ∠1 + ∠2 + ∠3 = 180°
Примеры для разных типов треугольников
| Тип треугольника | Пример углов | Сумма |
| Остроугольный | 60°, 60°, 60° | 180° |
| Прямоугольный | 90°, 45°, 45° | 180° |
| Тупоугольный | 120°, 30°, 30° | 180° |
| Разносторонний | 70°, 60°, 50° | 180° |
Практическое применение
В геометрии
- Нахождение неизвестного угла треугольника
- Доказательство других геометрических теорем
- Решение задач на построение
В технике
- Расчет углов в строительных конструкциях
- Проектирование механических деталей
- Компьютерная графика и 3D-моделирование
Исключения и особые случаи
Неевклидова геометрия
В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а в геометрии Римана - всегда больше 180°.
На сфере
Для сферических треугольников сумма углов превышает 180° и может достигать 540°.
Как найти неизвестный угол
Если известны два угла треугольника, третий можно найти по формуле:
∠C = 180° - (∠A + ∠B)
Пример расчета
- Дано: ∠A = 45°, ∠B = 60°
- Решение: ∠C = 180° - (45° + 60°) = 75°
Историческая справка
Данное свойство треугольников было известно еще древнегреческим математикам. Евклид использовал его как основу для многих доказательств в своих "Началах".
Заключение
Сумма внутренних углов треугольника, равная 180 градусам, является одним из краеугольных камней евклидовой геометрии. Это простое, но мощное свойство находит множество применений как в теоретической математике, так и в практических расчетах. Понимание этой закономерности необходимо для решения широкого круга геометрических задач.
